Question

Find the zeros of the function.
f(x) = 9x^3 - 45x^2 + 36x

Answer 1

x=0

x=1

x=4

Explanation:

Answer 2

The zeros of the function f(x) = 9x^3 - 45x^2 + 36x is 0, 1, 4

Solution:

Given that
`f(x)=9 x^(3)-45 x^(2)-36 x`

For finding the zeros of the function, we equate the entire function to zero i.e.,

`0=9 x^(3)-45 x^(2)+36 x`

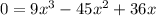
Dividing throughout by 9, we get

`0=x^(3)-5 x^(2)+4 x`

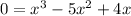
Taking x as common throughout the equation, we get

`0=x\left(x^(2)-5 x+4\right)`

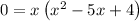
Thus, by factorization of the above equation, we get 0 = x(x - 1)(x - 4)

Now ,equating the factors we got to 0, we get

x = 0, x - 1 = 0, x - 4 = 0

x = 0, x = 1, x = 4

Thus, the zeros of the above given function are 0, 1, 4