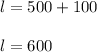Question

Two planes simultaneously left the Washington and LA and headed towards each other. The distance between the cities is 2700 miles. After they flied for 2 hours, they have not met each other yet, and distance between them was still 500 miles. What is the speed of each plane, if the one from LA was 100 mph faster?

Answer 1

Speed of the plane from Washington:
`500\ mph`

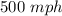
Speed of the plane from LA:
`600\ mph`

Explanation:

We need to remember that:

`d=Vt`

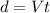
Where "d" is distance, "V" is speed and "t" is time.

Let be "w" the speed in mph of the plane from Washington and "l" the speed in mph of the plane from LA.

We know that the distance between the cities is 2700 miles and after they flied for 2 hours, the distance between them was 500 miles. Then we can write the following equation:

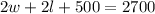`2w + 2l + 500 = 2700` [Equation 1]

Since the speed of the plan from LA was 100 mph faster, we can write this equation:

`l=w+100` [Equation 2]

The steps to solve this are:

1. Substitute the Equation 2 into the Equation 1 and solve for "w":

`2w + 2(w+100) + 500 = 2700\\\\4w+200+500=2700\\\\w=(2000)/(4)\\\\w=500`

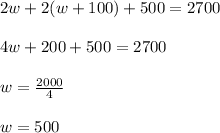
2. Substitute the value of "w" into the Equation 2 in order to find "l":

`l=500+100\\\\l=600`