Answer:
x = 49.84
Explanation:
We are given an equation of unknown x and we have to solve the equation for x.
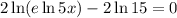
⇒
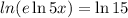
⇒
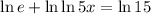 {Since we know that ln AB =ln A + ln B}
{Since we know that ln AB =ln A + ln B}
⇒
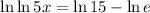
⇒
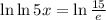 {Since we know that ln A/B = ln A - ln B}
{Since we know that ln A/B = ln A - ln B}
⇒
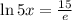
⇒
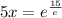
⇒
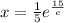 {Converting logarithm to exponent form}
{Converting logarithm to exponent form}
⇒ x = 49.84 (Approximate) (Answer)