Question

Solve the following system.
y=(-)x2 + 2x - 1 and 3x - y=1
The solutions are _and_

Answer 1

Since the coefficient of the quadratic variable is missing, I obtained it from a similar question.

The system is:

• y = (1/2)x² + 2²x - 1 and 3x - y = 1

Answer:

• The two solutions are (0, -1) and (2, 5)

Step-by-step explanation:

1. Write the system

`y=(1/2)x^2+2x-1\\ \\ 3x-y=1`

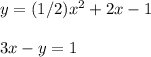
2. Clear y from the second equation to solve by substitution

`y= 3x-1`

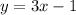
3. Substitute in the first equation and solve for x

`3x-1=(1/2)x^2+2x-1\\ \\ (1/2)x^2+2x-3x=0\\ \\ (1/2)x^2-x=0\\ \\ x(x/2-1)=0`

`x=0`

`x/2-1=0\\ \\ x/2=1\\ \\ x=2`

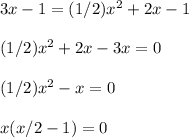
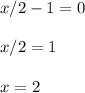
4. Subsitute both values into the equation y= 3x - 1

• y = 3(0) - 1 = - 1 ⇒ solution (0, -1)

• y = 3(2) - 1 = 5 ⇒ solution (2, 5)