Question

in an atwood’s machine, the larger mass is 4.2 kg and the smaller mass is 1.5 kg. Ignoring friction, what is the acceleration of the masses?

Answer 1

The acceleration of the masses in an Atwood's machine is 1.96 m/s².

Step-by-step explanation:

The acceleration of the masses in an Atwood's machine can be calculated using the formula:

acceleration = (m₂ - m₁) * g / (m₂ + m₁)

where m₁ is the mass of the smaller mass and m₂ is the mass of the larger mass, and g is the acceleration due to gravity (approximately 9.8 m/s²).

In this case, the smaller mass is 1.5 kg and the larger mass is 4.2 kg. Plugging in these values, we get:

acceleration = (4.2 kg - 1.5 kg) * 9.8 m/s² / (4.2 kg + 1.5 kg) = 1.96 m/s²

Therefore, the acceleration of the masses is 1.96 m/s².

Answer 2

a = 4.64 m/s²

Step-by-step explanation:

Given that,

Larger mass, M = 4.2 Kg

Smaller mass, m = 1.5 Kg

Friction of pulley = 0

Acceleration of the masses, a = ?

In an Atwood's machine,

Tension in the string, T

Acceleration due to gravity, g

The net force on the smaller mass is, f = T - mg ( f = ma)

The net force on the larger mass is, F = Mg -T (F = Ma)

Since the acceleration 'a' of the two masses remains the same, the equations can be solved to a.

Adding the above equations

ma + Ma = Mg -mg

a (m + M) = (M - m) g

`a = (M - m)/( M + m) g`

Substituting the values in the above equation

`a = (4.2 - 1.5)/( 4.2 + 1.5) 9.8`

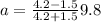
= 4.64 m/s²

Hence, the acceleration of the masses, a = 4.64 m/s²