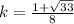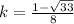Question

3. Determine k so that the given equation will have the stated property, and write the resulting equation:

(a) x
2 + 4kx + k + 2 = 0 has one root

Answer 1

The values of k are

`k=(1+√(33))/(8)`

`k=(1-√(33))/(8)`

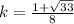
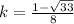
Explanation:

we know that

In a quadratic equation of the form

`ax^(2) +bx+c=0`

The discriminant D is equal to

`D=b^(2)-4(a)(c)`

If D=0 ----> The quadratic equation has only one real solution

If D>0 ----> The quadratic equation has two real solutions

If D<0 ----> The quadratic equation has no solutions (complex solutions)

in this problem we have

`x^(2) +4kx+k+2=0`

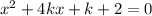
so

`a=1\\b=4k\\c=(k+2)`

Find out the discriminant D

substitute the values

`D=(4k)^(2)-4(1)(k+2)`

`D=16k^(2)-4k-8`

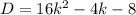
For D=0

`16k^(2)-4k-8=0`

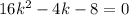
Solve for k

`16k^(2)-4k=8`

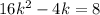
Factor 16 left side

`16(k^(2)-(1)/(4)k)=8`

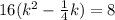
Complete the square

`16(k^(2)-(1)/(4)k+(1)/(64))=8+(1)/(4)`

`16(k^(2)-(1)/(4)k+(1)/(64))=(33)/(4)`

`(k^(2)-(1)/(4)k+(1)/(64))=(33)/(64)`

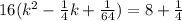
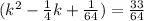
Rewrite as perfect squares

`(k-(1)/(8))^(2)=(33)/(64)`

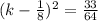
square root both sides

`k-(1)/(8)=(+/-)(√(33))/(8)`

`k=(1)/(8)(+/-)(√(33))/(8)`

`k=(1)/(8)(+)(√(33))/(8)=(1+√(33))/(8)`

`k=(1)/(8)(-)(√(33))/(8)=(1-√(33))/(8)`

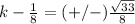
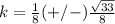
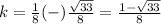
therefore

The values of k are

`k=(1+√(33))/(8)`

`k=(1-√(33))/(8)`