Question

A college student and $72,000 during summer vacation working as a waiter in the restaurant on the boardwalk at the beach. The student invested part of the money at 10% and the rest at 9%. If the student received a total of $680 in interest at the end of the year, how much was invested at 10%?

Answer 1

$3,200

Explanation:

The information "72,000" should be "7200".

Basically the question is

"7200 invested in 2 accounts, 10% and 9% interest accounts. After 1 year, interest earned is 680. So much was invested in 10% account??"

let amount invested in 10% be x

let amount invested in 9% be y

The formula is:

`SI=Prt`

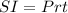
Where

SI is simple interest

P is the amount invested

r is the rate of interest (in decimal. percentage divided by 100 is decimal)

t is the time [here, t = 1, since after 1 year]

So, the equation can be written as:

x(0.10)(1) + y(0.09)(1) = 680

Also, y = 7200 - x

Substituting we get:

x(0.10) + (7200 - x)(0.09) = 680

Now we can solve for x:

`x(0.10) + (7200 - x)(0.09) = 680\\0.1x+648-0.09x=680\\0.01x=32\\x=(32)/(0.01)\\x=3200`

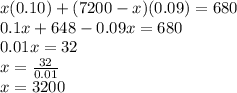
Thus, $3,200 was invested in 10%