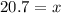Question

What is the value of x by rounding to the nearest tenths​

Answer 1

x = 20.7

Explanation:

1) Use the Pythagorean Theorem:
`a^(2) +b^(2) =c^(2)`

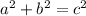
- C is always the hypotenuse of the triangle (The longest side in a right triangle)

2) Plug in 17.5 for A and 11 for B to make
`17.5^(2) +11^(2) =x^(2)`

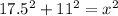
3) You should end up with
`306.25 +121 =x^(2)`

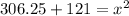
4) Add the two numbers to get
`427.25=x^(2)`

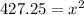
5) Take the square root of both sides of the equation:
`√(427.25) =\sqrt{ x^(2) }`

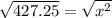
6) You will end up with a number with many decimals, but if rounding to the nearest tenth (one decimal place), you will find that
`20.7=x`

Answer 2

x = 20.7

Explanation:

So this is Pythagorean's Theorem

`a^(2)+b^(2) = c^(2)`

`}17.5^(2)+11^(2)=c^(2)` = 306.25 + 121 =
`c^(2)`

427.25 =
`c^(2)`

So we find the square root

c = 20.67003

To the nearest tenth it is 20.7