Question

HELP PLEASE!!!!!!!!!!!!

Answer 1

See the explanation.

Explanation:

We are given the function f(x) = x² + 2x - 5

Zeros :

If f(x) = 0 i.e. x² + 2x - 5 = 0

The left hand side can not be factorized. Hence, use Sridhar Acharya formula and

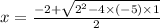`x= \frac{-2+\sqrt{2^(2)-4*(-5)*1 } }{2}` and

`x= \frac{-2-\sqrt{2^(2)-4*(-5)*1 } }{2}`

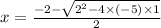
⇒ x = -3.45 and 1.45

Y- intercept :

Putting x = 0, we get, f(x) = - 5, Hence, y-intercept is -5.

Maximum point :

Not defined

Minimum point:

The equation can be expressed as (x + 1)² = (y + 5)

This is an equation of parabola having the vertex at (-1,-5) and axis parallel to + y-axis

Therefore, the minimum point is (-1,-5)

Domain :

x can be any real number

Range:

f(x) ≥ - 6

Interval of increase:

Since this is a parabola having the vertex at (-1,-5) and axis parallel to + y-axis.

Therefore, interval of increase is +∞ > x > -1

Interval of decrease:

-∞ < x < -1

End behavior :

`f(x) = x^(2) +2x-5 =x^(2)  (1+(2)/(x) -(5)/(x^(2) ) )`

So, as x tends to +∞ , then f(x) tends to +∞

And as x tends to -∞, then f(x) tends to +∞. (Answer)