Question

Write the equation in standard form of a circle with center (-7,2), tangent to the y-axis.

Answer 1

`(x+7)^(2)+ (y-2)^(2)=49`

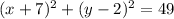
Explanation:

It is given that circle is a tangent to y axis, which tells us that the distance between the centre point and y axis is the radius of the triangle.

Formula for equation of circle with centre (x1,y1) and radius r is

`(x-x1)^(2)+ (y-y1)^(2)=r^(2)`

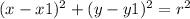
In the given case distance between the centre and y axis is 7 units so radius would be 7 and the centre point is (-7,2),

the equation of circle is ,

`(x+7)^(2)+ (y-2)^(2)=7^(2)`

`(x+7)^(2)+ (y-2)^(2)=49`

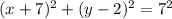
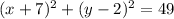
Hence the abow equation is the circle equation.