Question

Does anyone know how to do this?!?

Answer 1

77.6°

Explanation:

Looking at Triangle CDB, we see that we have an adjacent side and its angle. Let's say we want to find CD (because this is common to both). Side CD is "opposite" to the angle given and we have the side that is "adjacent". Which trigonometric ratio relates "opposite" with "adjacent" ??

That's TAN. Thus we can write:

`Tan(38)=(Opposite)/(Adjacent)=(CD)/(3.5)\\CD=Tan(38)*3.5CD=2.73`

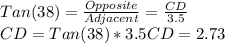
Now, looking at Triangle ADC. Since we now have side "opposite" of the angle and we know the "hypotenuse" (2.8), we can use another trig ratio.

Which trig ratio relates "opposite" and "hypotenuse" ??

Yes, its SINE. Thus, we can write:

`Sin(x)=(Opposite)/(Hypotenuse)=(2.73)/(2.8)=0.9766\\x=Sin^(-1)(0.9766)\\x=77.58`

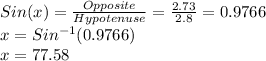
Rounded to 1 decimal place, that is 77.6°