Question

How do you simplify rational expressions?​

Answer 1

The simplification of rational expressions is explained

Solution:

Rational expressions are fractions that have a polynomial in the numerator, denominator, or both.

Rational expressions contain variables, they can be simplified in the same way that numerical fractions are simplified.

Steps to simplify rational expressions:

Let us see it with an example:

`(3 x^(2)-3 x)/(3 x^(3)-6 x^(2)+3 x)`

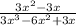
1) Look for factors that are common to the numerator & denominator

`(3 x(x-1))/(3 x\left(x^(2)-2 x+1\right))`

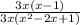
2) 3x is a common factor to the numerator & denominator. Note that it is clear that x ≠0

3) Cancel the common factor

`(x-1)/(x^(2)-2 x+1)`

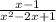
4) If possible, look for other factors that are common to the numerator and denominator

`(x-1)/((x-1)(x-1))`

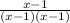
5) After cancelling, you are left with
`(1)/((x-1))`

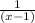
6) The final simplified rational expression is valid for all values of "x" except 0 and 1

We have to follow the same procedure for any rational expression.