Question

Prove that triangle AWM is congruent to triangle CPM using a two column proof

Answer 1

ΔAWM ≅ ΔCPM proved

Explanation:

See the given diagram with this question.

We have to prove ΔAWM ≅ ΔCPM

Now, (i) M is the mid point of AC, so AM =MC

(ii) Now, W is the mid point of AB, hence, AW = WB =
`(1)/(2) AB`

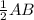
Again, P is the mid point of BC i.e
`BP = PC = (1)/(2) BC`

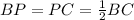
Now, it is given that BP = PM = MW = WB

Hence, BP = WB , hence, AW = PC

(iii) Again, PM = MW

Therefore, from the SSS rule, it is proved that ΔAWM ≅ ΔCPM. (Answer)