Question

6. The vertices of ALMN are L(7,4), M(7,16), and

N(42, 4).
a. Find the length of each side of the triangle.
b. What is the perimeter of the triangle?
C. What is the area of the triangle? Explain how
you determined your answer.​

Answer 1

(a) LM=12 units, LN=35 units, MN=37 units

(b)8 84 units

(c) 210 square units

Explanation:

(a)

Since points L and M have same x coordinates, it means they are in the same plane. Also, since the Y coordinates of L and N are same, they also lie in the same plane

Length
`LM=\sqrt {(7-7)^(2)+(16-4)^(2)}=12 units`

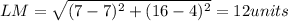
Length
`LN=\sqrt {(42-7)^(2)+(4-4)^(2)}=35 units`

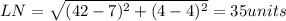
Length
`MN=\sqrt {(42-7)^(2)+(4-16)^(2)}=37 units`

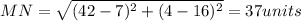
Alternatively, since this is a right angle triangle, length MN is found using Pythagoras theorem where

`MN=\sqrt {(LN)^(2)+(LM)^(2)}=\sqrt {(12)^(2)+(35)^(2)}=37 units`

Therefore, the lengths LM=12 units, LN=35 units and MN=37 units

(b)

Perimeter is the distance all round the figure

P=LM+LN+MN=12 units+35 units+37 units=84 units

(c)

Area of a triangle is given by 0.5bh where b is base and h is height, in this case, b is LN=35 units and h=LM which is 12 units

Therefore, A=0.5*12*35= 210 square units