Question

Triangle E D F has sides that are of varying lengths. Side E D has a length of 4 and side E F has a length of 9.

Which statements about the diagram are true? Select three options.

D E + E F greater-than D F
Triangle D E F is an isosceles triangle.
5 less-than D F less-than 13
D E + D F less-than E F
Triangle D E F is a scalene triangle.

Answer 1

DE + EF > DF

5 < DF < 13

Triangle DEF is a scalene triangle

Explanation:

Got it right on Edge.

Answer 2

D E + E F greater-than D F

5 less-than D F less-than 13

Triangle D E F is a scalene triangle

Explanation:

we know that

The Triangle Inequality Theorem states that the sum of any 2 sides of a triangle must be greater than the measure of the third side

we have the triangle EDF

where

`ED=4\ units\\EF=9\ units`

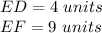
Applying the triangle inequality theorem

1)

`ED+EF > DF\\4+9 > DF\\13 > DF\\DF < 13\ units`

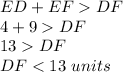
2)

`ED+DF > EF\\4+DF > 9\\DF > 5\ units`

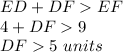
so

The length of DF is the interval -----> (5,13)

The triangle DEF is a scalene triangle (the three length sides are different)

therefore

The statements that are true are

D E + E F greater-than D F

5 less-than D F less-than 13

Triangle D E F is a scalene triangle