Question

How much money will there be in an account at the end of 10 years if ​$150,00 is deposited at 3% compounded quarterly?​

(Assume no withdrawals are​ made.)

Answer 1

Explanation:

Use the formula

`A(t)=P(1+(r)/(n))^((n)(t))`

where A(t) is the amount of money in the account after a certain number of years, P is the amount invested initially, r is the interest rate in decimal form, n is the number of times the interest compounds per year, and t is the time in years. Filling in:

`A(t)=150,000(1+(.03)/(4))^((4)(10))`

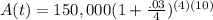
Simplifying a bit:

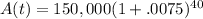`A(t)=150,000(1+.0075)^(40)` and a bit more:

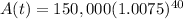`A(t)=150,000(1.0075)^(40)` and a bit more still:

A(t) = 150,000(1.348348612) so

A(t) = 202,252.29