Question

Water is being drained out of a swimming pool at a constant rate of 780 gallons per hour. The swimming pool initially contained 45,000 gallons of water. A chemical additive must be added to the pool when it has no more than 15,000 gallons of water remaining in the pool.

1. Write an equation for the amount of water remaining in the pool after h-hours.
2. Write an equation that could be solved to find the least number of hours before the chemical could be added.
3. Will it take longer than 2 days before the check am can be added? Justify your response.

Answer 1

1.
`W_(R) = 45000 -780h`

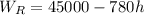
2. 15000 = 45000 -780h

3. Less than 2 days.

Explanation:

1. If h is the number of hours that the water is drained out for then at the rate of 780 gallons per hour total of 780h gallons of water will be drained out. If there were 45000 gallons of water initially in the swimming pool, then the equation for the amount of water remaining in the pool after h hours will be given by

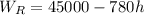`W_(R) = 45000 -780h` ....... (1) (Answer)

2. Given that when there are no more than 15000 gallons of water remaining in the pool a chemical additive must be added in the water.

Therefore, from equation (1), we have

15000 = 45000 -780h ........(2) (Answer)

3. Solving equation (2), we get h = 38.46 hours < 2 days i.e 48 hours.

So, it will not take longer than 2 days before the chemical can be added. (Answer)