For this case we propose a system of equations:
x: Let the variable representing the cost of each pizza slice
y: Let the variable that represents the cost of each drink
According to the data we have:
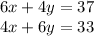
We multiply the first equation by -4:
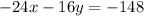
We multiply the second equation by 6:
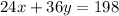
We add the equations:

So, each drink costs $2.5
For its part, each slice costs:
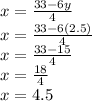
Each slice cuests $4.5
Answer:
Each drink costs $2.5
Each slice cuests $4.5