Question

The equation of a circle is ( x - 3) 2 + ( y + 2) 2 = 25. The point (8, -2) is on the circle.

What is the equation of the line that is tangent to the circle at (8, -2)?

y = 8
x = 8
x = 3
y = 3

Answer 1

x =8 Is The Equation Of The Tangent.

Step-by-step explanation: Hope This Helps You!!! <3

Answer 2

x =8 is the equation of the tangent.

Explanation:

Here the equation of the given circle is:
`(x-3)^(2)  + (y+2)^(2)  = 25`

Now, comparing it with the general equation of circle:
`(x-h)^(2)  + (y -k)^(2)  = r^2`

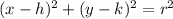
we get the central coordinates (h,k) = (3,-2)

So, the slope of the line joining center and (8, -2) =
`(-2 -(-2))/(8-3) = (0)/(5) = 0`

Since the slope of line = 0, line is parallel to x axis.

Now, as tangent and the line is perpendicular to each other

⇒Slope of the tangent = -1/ slope of the line =
`(-1)/(0)`

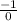
Now, by point slope formula: the equation of the tangent is

(y-y0) = m (x-x0)

or,
`(y +2) = (-1)/(0) (x -8)`

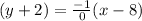
or x =8 is the equation of the tangent.