Question

Verifying Parallel and Perpendicular Lines using Slope

Use the diagram to answer the questions.
Is line m parallel to line n? Explain.
Is line m perpendicular to line k? Explain.

Answer 1

1) No, the slopes are not equal

2) Yes, the slopes are negative reciprocals

Explanation:

Answer 2

The line m and line n are not parallel to each other.

line m ⊥ line k.

Explanation:

See the diagram attached to this question.

The points (0,-4) and (-4,3) through which line m passes.

Therefore, the slope of line m is
`(-4-3)/(0-(-4)) =-(7)/(4)`

Now, line n passes through the points (1,2) and (3,-2).

Therefore, the slope of the line n is
`(2-(-2))/(1-3)=-2`

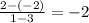
Hence, the line m and line n are not parallel as their slopes are not equal. (Answer)

Again, the points (4,1) and (-3,-3) through which line k passes.

Therefore, the slope of the line k is
`(1-(-3))/(4-(-3)) =(4)/(7)`

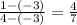
Hence, the product of slopes of line m and line k is
`(-(7)/(4)) * ((4)/(7) )  =-1`.

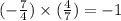So, line m ⊥ line k. (Answer)

{Since -1 will be the result if we multiply the slopes of two mutually perpendicular straight lines }