Question

What is an equation of the line that passes through the point (-5, -6) and is

perpendicular to the line x + 2y = 2?

Answer 1

Answer: y= 2x +4

Explanation:

1. To be able to write the equation of the line, you want to be able to find the slope first. To do so, rearrange the given equation x+2y=2 into slope-intercept form, which is y=mx+b

First subtract x from both side, which will give us 2y=2-x. Rearrange this to get 2y= -x+2. Then, divide both sides by 2. This will give us y= -1/2x+1

2. Now that you have the equation, look for the slope in the new equation; this will be the m value. In this case, the slope is -1/2. Since we are looking for a line that is perpendicular, we have to change the slope so that it is the opposite reciprocal. The opposite reciprocal of -1/2 is 2, so the slope of the equation we want to find is 2.

3. Next, all we have to do is plug the given ordered pair (-5, -6) and the slope that we found (m=2) into the point-slope equation, which is
`y-y_(1) = m(x-x_(1) )`

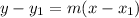
That will give us:

y+6 = 2(x+5)

4. Now, solve this equation.

y+6 = 2(x+5) --> distribute the 2 inside the parentheses

y+6 = 2x + 10 --> subtract 6 from both sides

y= 2x +4