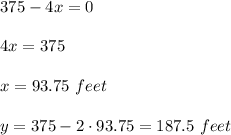Answer:
93.75 feet and 187.5 feet
Explanation:
Let the width of the rectangular area be x feet and the length be y feet. A farmer with 750 feet of fencing wants to enclose a rectangular area and then divide it into three pens with fencing parallel to one side of the rectangle. So, there will be 4 widths and 2 lengths, thus
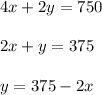
Find the area:

Find the derivative:
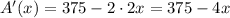
Equate it to 0: