Question

Highschool level trigonometry!!! Need help knowing step by step how to find answer!

A ladder is 15 m long. The top of the ladder rests against the wall of a house, and the foot rests on level ground 2m from the wall. Draw a diagram to illustrate the situation. Calculate the angle between the ladder and the ground.

Answer 1

`\theta \approx 82.34^\circ`

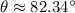
Explanation:

Please refer to the attached diagram. (Apologies if the shading or resolution is a bit off.)

So, we want to find θ.

Since we formed a right triangle, we can use right triangle ratios.

We know the measure of the adjacent side to θ and the hypotenuse.

Therefore, we will use the cosine ratio:

`\displaystyle \cos(\theta)=\frac{\text{adjacent}}{\text{hypotenuse}}`

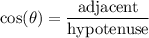
The adjacent side is 2 and the hypotenuse is 15. By substitution:

`\displaystyle \cos(\theta)=(2)/(15)`

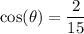
Now, we will take the inverse cosine of both sides. So:

`\displaystyle \theta=\cos^(-1)\Big((2)/(15)\Big)`

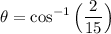
Use a calculator. Hence:

`\theta \approx 82.34^\circ`

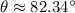
The angle between the ground and the ladder is about 82.34°.