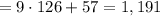Answer:
Tickets sold:
VIP
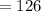
$17 tickets
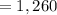
$21 tickets
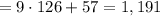
Explanation:
Let x be the number of VIP tickets.
If ten times as many $17 tickets were sold as VIP tickets, then the number of $17 tickets is
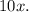
If the number of $17 tickets sold was 57 more than the sum of the number of $21 tickets and VIP tickets, then
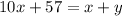 and the number y of $21 tickets is
and the number y of $21 tickets is
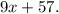
Amounts earned:
VIP tickets
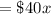
$17 tickets

$21 tickets

Total
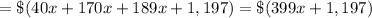
The sales of all three kinds of tickets would total $51,471, so
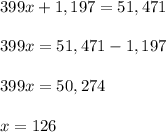
Tickets sold:
VIP
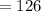
$17 tickets
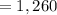
$21 tickets