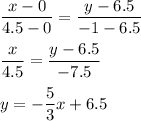Answer:
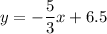
Explanation:
Given: trapezoid RSTU with vertices R(-1, 5), S(1, 8), T(7, -2), and U(2, 0).
Plot these points on the coordinate plane. As you can see, lines RU and ST are parallel lines and segments ST and RU are bases of the trapezoid.
The median of the trapezoid (the middle line) passes through the midpoints of the sides RS and TU. Find these midpoints:
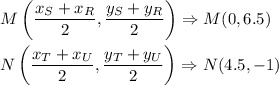
The equation of the line MN is