Question

In the first week of August, there were 1,060 people at an amusement

park. In the second week, there were 848 people. In the third week, there
were 1,272 people. In the fourth week, only 318 people went to the
amusement park. What is the percent of change in the number of people
who went to the amusement park for each week in August? Tell whether
each week was a percent increase or decrease from the week before.

Answer 1

The percent of change in attendance at the amusement park for each week in August showed a 20% decrease from the first to the second week, a 50% increase from the second to the third week, and a 75% decrease from the third to the fourth week.

Step-by-step explanation:

To calculate the percent of change in attendance at the amusement park for each week in August, we’ll use the formula:

Percent Change = [(New Value - Original Value) / Original Value] × 100%

Let's calculate the percent change for each week compared to the previous one:

1. Week 2: 848 - 1,060 = -212; Percent Change = (-212 / 1,060) × 100% ≈ -20%
2. Week 3: 1,272 - 848 = 424; Percent Change = (424 / 848) × 100% ≈ 50%
3. Week 4: 318 - 1,272 = -954; Percent Change = (-954 / 1,272) × 100% ≈ -75%

From Week 1 to Week 2, there was a 20% decrease. From Week 2 to Week 3, there was a 50% increase. And from Week 3 to Week 4, there was a 75% decrease in attendance.

Answer 2

In second week there is percentage decrease (-ve sign) of 20% in people visiting compare to first week.

In third week there is percentage increase of 50% in people visiting compare to second week.

In fourth week there is percentage decrease of 75% in people visiting compare to third week.

Solution:

Need to determine percentage change in the number of people who went to amusement park for each week in august.

Given that,

In first week of august number of people went to amusement park let say
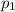`p_1` = 1060

In second week of august number of people went to amusement park let say
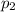`p_2` = 848

In third week of august number of people went to amusement park let say
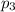`p_3` = 1272

And in fourth week of august number of people went to amusement park let say
`p_4` = 318

Percentage change from first week to second week is as follows

`\% \text { change }=(p_(2)-p_(1))/(p_(1)) * 100=(848-1060)/(1060) * 100`

`=(-212)/(1060) * 100=-20 \%`

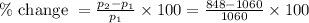
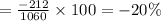
So in second week there is percentage decrease (-ve sigh) of 20% in people visiting compare to first week.

Percentage change from second week to third week is as follows

`\begin{aligned} \% \text { change }=(p_(3)-p_(2))/(p_(2)) * 100 &=(1272-848)/(848) * 100 =(424)/(848) * 100=50 \% \end{aligned}`

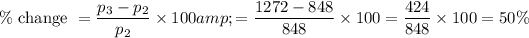
So in third week there is percentage increase of 50% in people visiting compare to second week

Percentage change from third week to fourth week is as follows

`\begin{aligned} \% \text { change }=& (p_(4)-p_(3))/(p_(3)) * 100=(318-1272)/(1272) * 100 =(-954)/(1272) * 100=-75 \% \end{aligned}`

So in fourth week there is percentage decrease of 75% in people visiting compare to third week