Question

Given that f(x)=3x+2 and g(x)=x^2-3x-6, find (gof)(6)

Answer 1

(gof)(6) = 334

Explanation:

The expression "(gof)(6)" means a composite function. Putting one function into another and then evaluating.

Thus,

(gof)(6) means "Put the function f into g and get a new function (gof)(x). Then put 6 into x of that new function and thus we get (gof)(6)"

So, let's find (gof)(x) first. Shown below:

`(gof)(x) = (3x+2)^2-3(3x+2)-6`

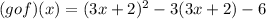
Now, we simplify:

`(gof)(x) = (3x+2)^2-3(3x+2)-6\\=9x^2+12x+4-9x-6-6\\=9x^2+3x-8`

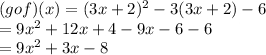
Now, we plug in 6 into x and evaluate:

`(gof)(x)=9x^2+3x-8\\(gof)(6)=9(6)^2+3(6)-8\\(gof)(6)=334`

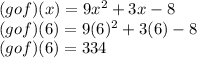
Thus, the value is 334