Question

Find if this function is surjective or injective : f(x) =e^x​

Answer 1

The function is both injective and surjective.

Explanation:

Given function,

`y=e^x`

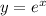
We say a function is injective(one-one) when for every value of x we have a unique value of y.We say a function is surjective(onto) when the output y covers all the values of the co domain.

We know that in the graph of
`e^x` at no two points of x there can be a common y. So hence proved that
`e^x` is injective.

`e^x` is also surjective because for x from - infinity to + infinity
`e^x` covers all the values in its co domain hence it is also surjecctive function.