Answer:
Option B:
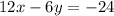
Explanation:
A function is said to be increasing if it has a slope greater than 0.
The function with the largest slope has the highest increasing rate.
Here, for the graph in option A, the function is decreasing with increasing
 . So, it has a negative slope.
. So, it has a negative slope.
We need to convert equation of option B into standard form and then determine its slope.
The standard form of a straight line is
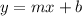 , where
, where
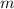 is the slope of the line and
is the slope of the line and
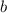 is the y-intercept.
is the y-intercept.
Now, given function is:
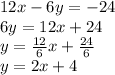
Therefore, the slope is 2.
Option C:
Slope is given as,
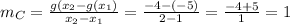
Therefore, the slope is 1.
Option D:
Equation of a line with
 and
and
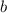 as
as
 and
and
 intercepts is given as,
intercepts is given as,
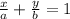
Here,
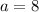 and
and
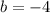
∴
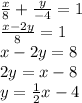
Therefore, the slope is
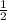 .
.
Hence, the largest slope is for option B and thereby the highest increasing rate.