Question

a man can row about 4kmperhr in a still water.he rows the boat 2km up the stream and 2km back to his starting point in 2hr.how fast is the stream flowing. ​

Answer 1

The stream flowing at a speed of
`2.828 \mathrm{km} / \mathrm{hr}`

Step-by-step explanation:

Given:

Distance = 2km (both in upstream and downstream)

The speed in still water be x km/hr.

The speed in upstream = 4-x

Speed in downstream = 4+x

Solution:

We know that, Speed = distance/time

So, Time = distance/speed

Therefore,

`2=\left((2)/(4-x)\right)+\left((2)/(4+x)\right)`

`2=(2(4+x)+2(4-x))/((4-x)(4+x))`

`2(4-x)(4+x)=2(4+x)+2(4-x)`

`2(4-x)(4+x)=2(4+x+4-x)`

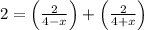
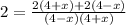
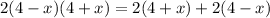
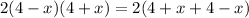
By cancelling 2 on both sides,

`16-x^(2)=8`

`x^(2)=16-8=8`

`x=√(8)`

`x=2.828 \mathrm{km} / \mathrm{hr}`

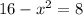
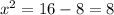
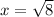
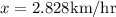
Result:

Thus the speed of the stream is
`2.828 \mathrm{km} / \mathrm{hr}`