Answer:
A quadrilateral become square if all the sides joining the co-ordinate of quadrilateral is equal
Explanation:
Here the given co-ordinate of quadrilateral are
G (3, -1) O(1, -6)
L(-4, -4) F(-2, 1)
Line GF =
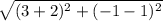
GF =
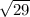
Similarly for line OG, OL, FL
OG =
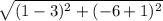
OG =
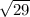
OL =
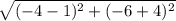
OL =
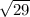
And
FL =
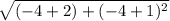
FL =
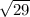
all the sides of quadrilateral GF, OG, OL, FL all equal to
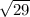
As all the sides are equal so quadrilateral become square Answer