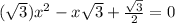Answer:
The equation is:
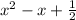
(A)
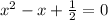
(B)
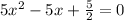
(C)
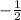
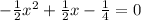
d) √3
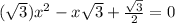
Explanation:
If the roots of the quadratic equation are:

This means:
x=
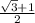 OR
OR
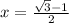
x-
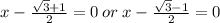 =0 or x-
=0 or x-
If a=0 or b=0, then ab=0
Therefore:
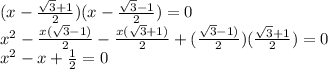
Therefore the coefficient of
 here is 1.
here is 1.
b) To make 5 the coefficient of

Simply multiply
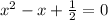 by 5
by 5
This gives:
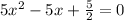
c)
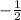
To make
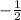 the coefficient of
the coefficient of

Simply multiply
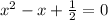 by
by
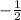
This gives:
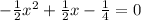
d) √3
To make
 the coefficient of
the coefficient of

Simply multiply
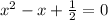 by
by

This gives: