Question

What amount of a 70% acid solution must be mixed with a 50% solution to produce 200 mL of a 60% solution?

Answer 1

100 ml of each solution

Explanation:

I calculated this by using this system of equations:

`x + y = 200`

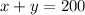
This first equation represents that units (mL) of the x value (the 70% solution) and the y value (the 50% solution) equals a total unit number of 200 (mL, in this case).

`(.7x + .5y) / 200 = .6`

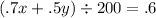
This second equation will find the average:

(ValueA+ValueB)/Units = Average

The .7 and .5 represent the % of the solution respectively, and x and y values are the units of each solution, then divided by the total amount of units (200), which equals .6, which is equal to 60%, which is the solution that is desired.

The first guess that comes to mind is 100 for both values, which apparently was correct.

If guessing is not allowed, simply use substitution, elimination, or graphing to figure it out.

One search on your search engine should help you out on the 3 main methods on solving systems of equations.