Answer:
The amount of 4% alloy were used to produce 32 kg of 16% alloy is 4
Step-by-step explanation:
let x kg be the amount of pure tin and y kg be the amount of 4% tin alloy mixed.
The weight of the mixture is 32 kg
then
 ----- -(1)
----- -(1)
there are 4% of tin in y kg of 4% tin alloy, so there are 0.04y kg of tin in this alloy.
There are 16% of tin in 32 kg of the mixture, then there are 0.16x0.32 = 5.12 kg of tin in alloy;
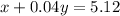 ------------------- - (2);
------------------- - (2);
solving (1) and (2)
we get,

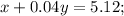
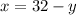
substituting in eq-(2)
we get;
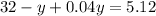
multiplying with 100 on both sides we get;
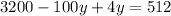
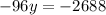
y=28
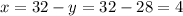
X=4