Answer:
The acceleration due to gravity on zarth = 0.8
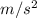
Step-by-step explanation:
The acceleration due to gravity on earth = 9.8
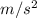
We know that time taken(t) by an object to fall a distance (d) is given by
t =
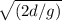
We are given the height from which the ball is dropped = 10m and the time taken by the ball to fall = 5.0s
So, substituting the given values
d = height of dropping the ball = 10m, t = 5.0 s
i.e. time taken for fall ,in the equation,
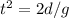
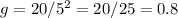
Therefore (g) = 0.8
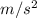 which gives the acceleration due to gravity on planet Zarth.
which gives the acceleration due to gravity on planet Zarth.