Question

A student would like to find the height of a statue. The length of the​ statue's right arm is 48 feet. The​ student's right arm is 2 feet long and her height is 5 1/3

feet. Use this information to find the height of the statue. How close is the approximate height to the​ statue's actual height of 128 ​feet, 3 inches from heel to top of​ head?

Answer 1

• Calculated (approximate) height ot the statue: 128 feet

• How close is the approximate height to the actual height: very close, with a small error of 3 in or 0.2%

Step-by-step explanation:

This problem is about proportions. A proportion an equality between two ratios.

In this case, you assume that the ratio of length of the student's right arm and his height is equal to the ratio of the statue's right arm and its height.

Let's use the following variables to work more neatly:

• Length of the student's right arm: A₁ = 2 ft

• Height of the studend: H₁ = 5 1/3

• Length of statue's right arm: A₂ = 48 ft

• Height of the statue: H₂ = x (unknown)

Proportion:

`(A_1)/(H_1) =(A_2)/(H_2)\\\\(2ft)/(5(1)/(3)ft ) =(48ft)/(x)`

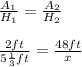
Convert the mixed number into improper fraction:

• 
  `5(1)/(3)=5+(1)/(3)=(15+1)/(3)=(16)/(3)`

Continue with the proportion:

`(2ft)/((16)/(3)ft ) =(48ft)/(x)\\ \\ x=(48.(16)/(3) )/(2)ft\\ \\ x=128ft`

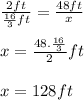
Thus, the calculated height of the statue is 128 feet.

Error:

To determine how close is the approximate height to the​ statue's actual height of 128 ​feet, 3 inches from heel to top of​ head, calculate the difference (absolute error):

• Absolute error = [128 feet + 3 inches] - [128 feet] = 3 inches.

So, the absolute error is 3 inches.

You can also calculate the percent error:

• Percent error = | Calculated value - True value / True value × 100

• Percent error = 3 in / [128 ft + 3in] × 100

• Percent error = 3 in / [1536 in + 3 in] × 100 = 3 in / 1539 in × 100

• Percent error = 0.19% ≈ 0.2% Which is a very low error and the approximation is very close to the actual height.