Answer:
If D< 0, the roots of the quadratic equation will b complex.
Explanation:
Let
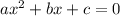 is the given quadratic equation.
is the given quadratic equation.
So, if the Discriminant (D) =
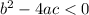 , the the equation will have only complex solutions.
, the the equation will have only complex solutions.
Complex roots are represented in the form of
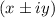
1. x represents the X axis (real) co ordinate,
y represents the Y axis (imaginary) coordinate
2. Also, the graph of the with equation D < 0 NEVER CROSSES the X - axis, as there are no real roots of the equation, only complex roots.
3. Here. roots are always identical but are opposite in signs. Such pair or roots with opposite sign are called CONJUGATE PAIRS.