Answer:
x - y = P - Q
Step-by-step explanation:
The equation of the line that is parallel to line g, will have the same slope as line g.
Find the slope of line g using two points on the line, (-3, 2) and (0, 5):
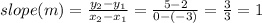
m = 1
Point-slope equation takes the form, y - b = m(x - a), where,
(a, b) is a point the line passes through
m = slope of the line
If the line parallel to g passes through (P, Q), then the equation can be written as follows:
Substitute (a, b) = (P, Q), and m = 1 into y - b = m(x - a).
Thus:
y - Q = 1(x - P)
y - Q = x - P
Rewrite
P - Q = x - y
x - y = P - Q