Question

Please solve this for me.
Thanks

Answer 1

10y = 13x + 139

Explanation:

Points (-5, -3) and (-15, -16) are the two points through which Line 1 passes.

So, the slope of the line 1 is
`(-3-(-16))/(-5-(-15)) =(13)/(10)`

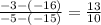
Now, the slope of the parallel straight line i.e. line 2 will be same as line 1 i.e.
`(13)/(10)`

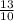
Let us assume that the equation of line 2 is

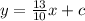`y= (13)/(10) x+c` {Where c is a constant} ....... (1)

Now, line 2 passes through the point (-13, 17). Hence, this point will satisfy equation (1).

So,
`17= (13)/(10) (-13)+c`

⇒
`c=(139)/(10)`

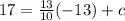
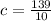
Therefore, the equation of line 2 will be

`y=(13)/(10) x+(139)/(10)`

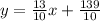
⇒ 10y = 13x + 139 (Answer)