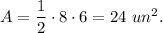Answer:
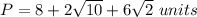

Explanation:
Plot the vertices of the triangle ABC on the coordinate plane and find the sides AB, BC and AC lengths:
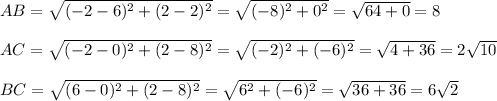
So, the perimeter of the triangle ABC is
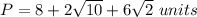
To find the area of the triangle, use the formula

In your case, AB is the base and the height is 6 units long (see attached diagram). Therefore,