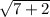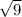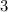Answer(there are assumptions for this answer that you need to confirm and look at):
Assumptions:
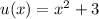 and
and
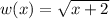
Answer if the operation is multiplication:
If you meant a closed dot which is the symbol for multiplication.

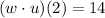
Answer if the operation is composition:
If you meant an open dot which is the symbol for composition.
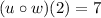
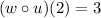
Note: I don't know if you actually meant
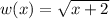 or if
or if
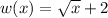 . Please let me know one way or the other.
. Please let me know one way or the other.
Explanation:
If we assume the functions are:
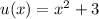
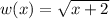
 since multiplication is commutative.
since multiplication is commutative.
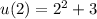
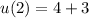


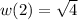
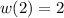
We are asked to find
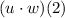 and
and
 .
.
The order doesn't matter in multiplication.
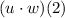
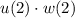
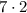
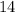

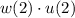
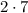
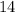
Now you might have meant composition which symbolized with an open circle, not a closed one.
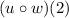
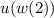
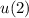 since
since
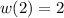
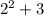
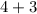
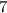


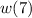 since
since