Answers:
A: Angular velocity

B: Linear velocity
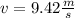
C: Linear Distance

Given:
Radius of the rope r=30cm=0.3m
Angular distance
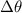 =10 revolutions
=10 revolutions
Time taken t=2seconds
To find:
A: Angular velocity in radians
B: Linear speed
C: Distance covered in 5 seconds
Step by Step Explanations:
Solution:
A: Angular velocity in radians;
According to the formula, Angular velocity can be calculated as
Angular Velocity = angular distance/ time
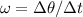
Where
 =Angular velocity
=Angular velocity
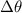 =Angular distance=10 revolutions
=Angular distance=10 revolutions
Changing revolutions to radians multiply with
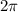 , so that we get
, so that we get
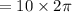
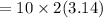
=62.80 rad/rev
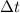 =Change in time
=Change in time
Substitute the known values in the above equation we get
 =62.80 / 2
=62.80 / 2

B. Linear speed of the rope;
As per the formula
Linear speed = angular speed × radius
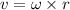
Where
 =Angular velocity
=Angular velocity
v=Linear speed of the rope
r=Radius of the rope
Substitute the known values in the above equation we get
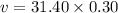
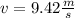
C. Dsitance covered in 5 seconds;
Linear distance = linear speed × time
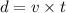
Where d= Linear distance of the rope
v=Linear speed of the rope
t=Time taken
Substitute the known values in the above equation we get
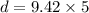

Result:
Thus A: Angular velocity of the rope

B Linear speed of the rope
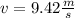
C: Distance covered in 5 seconds
