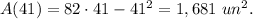Question

Among all rectangles that have a perimeter of 164, find the dimensions of the one whose area is largest. Write your answers

as fractions reduced to lowest terms.

Answer 1

The largest area is
`1,681\ un^2.` when the width is 41 units and the length is 41 units (when rectangle is a square)

Explanation:

Let x units be the width of the rectangle, y units be the length of the rectangle.

If the perimeter of the rectangle is 164 units, then

`2(x+y)=164\\ \\x+y=82\\ \\y=82-x\ units`

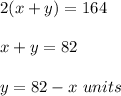
Find the area of the rectangle:

`A=xy\\ \\A(x)=x(82-x)\\ \\A(x)=82x-x^2`

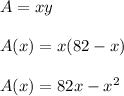
Find the derivative:

`A'(x)=(82x-x^2)'=82-2x`

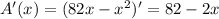
Equate it to 0:

`82-2x=0\\ \\2x=82\\ \\x=41\ units`

When x = 41 units, the area is the largest and is equal to

`A(41)=82\cdot 41-41^2=1,681\ un^2.`