Question

QUESTION 20

A 100 kg box is being pulled by a chain along a horizontal surface. The chain is at a 25° angle. The coefficient of friction between the box and surface is 0.46
The box starts from rest and travels 16 meters in 9 seconds. What is the acceleration, tension force and normal force for the box?
a) Acceleration
b) Normal Force
C) Tension Force

Acceleration = 0.4m/s2

Answer 1

a)
`0.4 m/s^2`

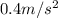
We can find the acceleration of the box by using the suvat equation:

`s=ut+(1)/(2)at^2`

where

s is the distance travelled

u is the initial velocity

t is the time

a is the acceleration

For the box in the problem,

s = 16 m

t = 9 s

u = 0 (it starts from rest)

Solving for a, we find the acceleration:

`a=(2s)/(t^2)=(2(16))/(9^2)=0.4 m/s^2`

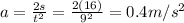
C) Tension force in the chain: 446 N

In order to find the normal force, we have to write the equation of the forces along the vertical direction.

We have 3 forces acting along this direction on the box:

- The normal force, N, upward

- The force of gravity, mg, downward (where m= mass of the box and g = acceleration of gravity)

- The vertical component of the tension of in the chain,
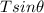`T sin \theta`, upward

So the equation of the forces along the vertical direction is

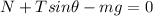`N+Tsin \theta - mg = 0` (1)

Along the horizontal direction, instead, we have the following equation:

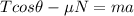`T cos \theta - \mu N = ma` (2)

where

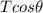`T cos \theta` is the horizontal component of the tension in the chain

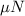`\mu N` is the frictional force

a is the acceleration

From (1) we write

`N=mg-T sin \theta`

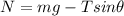
And substituting into (2),

`T cos \theta - \mu (mg-T sin \theta) = ma\\T cos \theta - \mu mg + \mu T sin \theta = ma\\T = (ma+\mu mg)/(cos \theta + \mu sin \theta)`

And substituting:

m = 100 kg

`\theta=25^(\circ)`

`\mu=0.46`

`a=0.4 m/s^2`

`g=9.8 m/s^2`

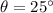
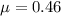
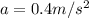
We find the tension in the chain:

`T = ((100)(0.4)+(0.46)(100)(9.8))/(cos 25 + 0.46 sin 25)=446 N`

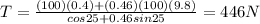
B) Normal force: 792 N

We can now find the normal force by using again equation (1):

`N+Tsin \theta - mg = 0`

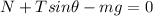
And substituting:

T = 446 N

m = 100 kg

`\theta=25^(\circ)`

`g=9.8 m/s^2`

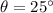
We find:

`N=mg-T sin \theta=(100)(9.8)-(446)(sin 25)=792 N`