Question

A company produces 3 types of widgets. On a given day, the company was able to produce 9 total widgets (combining all 3 types). Widget A costs $3 to produce, Widget B costs #2 to produce, and Widget C costs $1 to produce. The cost to produce the widgets each day is $18. The company produces one more Widget B than the sum of the Widgets A & C. How many of each type of Widget is produced?

Answer 1

Number of widgets A and C are 2 each, widgets B are 5.

Step-by-step explanation:

Let
`x` be the number of widgets A,
`y` be the number of widgets B and
`z` be the number of widgets C.

As per the question,

On a given day, total 9 widgets are produced. So,

`x+y+z=9`

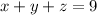
Cost for 1 widget A is $3. So, cost of
`x` widgets A is 3x.

Cost for 1 widget B is $2. So, cost of
`y` widgets A is 2y.

Cost for 1 widget C is $1. So, cost of
`z` widgets A is z.

Now, total cost of the widgets is $18. So,

`3x+2y+z=18`

Also, widget B is one more than the sum of widgets A and C. So,

`y=x+z+1`

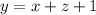
Now, we have 3 equations and 3 unknowns.

`x+y+z=9`

`3x+2y+z=18`

`y=x+z+1`⇒
`x+z=y-1`

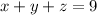
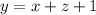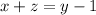
Now, using the first and third equation, we get

`y+y-1=9\\2y=10\\y=5`

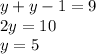
Plug in 5 for
`y` in the first 2 equations. This gives,

`x+5+z=9`⇒
`x+z=4`

`3x+2(5)+z=18`⇒
`3x+z=8`

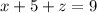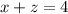
Subtracting the above 2 equations, we get,

`x-3x+z-z=4-8\\-2x=-4\\x=2`

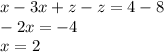
Using the value of x in the above equation, we find z.

`x+z=4\\2+z=4\\z=2`

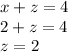
Therefore,
`x=2,y=5,z=2`

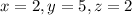
Hence, number of widgets A and C are 2 each, widgets B are 5.