Answer:
1 unit
Explanation:
See the attached diagram.
ΔABC is an isosceles triangle having ∠A = 36° and base angles ∠B = ∠C = 72°
Now, the bisector of angle B intersects AC at P.
Now, ∠ABP = 36° and ∠A = 36°, hence, ∠APB = 180° - 36° - 36° = 108°
Now, given that AB = AC = 1.618 units and BC = 1 unit
So, from the property of triangles of ΔABP, we have,
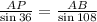
⇒
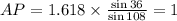 units (Approximate) (Answer)
units (Approximate) (Answer)