Question

A car moves along a road. While passing through a gas station, the driver sees a house on the right, the visual forms an angle of 39 ° on the direction of the road. Two minutes later he looks back and sees the house: now the angle is 65 °. If the house is 7km from the gas station (in the direction of the road), calculate the speed of the car

Answer 1

307.92 km per hour.

Explanation:

Let us assume that the distance from the road to the house is x km.

Now, for the case when the house is in front of the car,

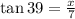`\tan 39 =(x)/(7)` {Since the distance from the gas station to the house is 7 km.}

⇒ x = 5.668 km.

Now, let us assume that when the driver sees the house to the back then it was y km from the house.

Hence,
`\tan 65 =(x)/(y) =(5.668)/(y)`

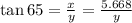
⇒ y = 3.264 km.

Therefore, the car moves by ( 7 + 3.264 ) = 10.264 km in 2 minutes {As per given condition}

Therefore, the speed of the car is
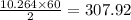`(10.264 * 60)/(2)=307.92` km per hour. (Answer)