Question

I NEED HELP PLEASE

The coordinates of the vertices of quadrilateral GOLF are G(3, -1), O(1, -6), L(-4, -4), and F(-2, 1). Prove or disprove that the quadrilateral is a square. Explanation is not necessary, but be sure to show all work.

Hint: Identify the characteristics of a square (there are 3). Use algebra to discover if this quadrilateral has those characteristics, or not.

Answer 1

It is proved that GOLF is a square.

Explanation:

If we can prove that all the sides of a quadrilateral are of equal length and any one of the angles is right angle then we will be able to say that the quadrilateral is a square.

Now, given four vertices of the quadrilateral GOLF as G(3, -1), O(1, -6), L(-4, -4), and F(-2, 1).

Hence, length of GO is
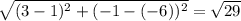`\sqrt{(3-1)^(2)+(-1-(-6))^(2)  } =√(29)` units.

Length of OL is
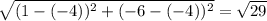`\sqrt{(1-(-4))^(2)+(-6-(-4))^(2)  } =√(29)` units.

Length of LF is
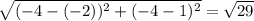`\sqrt{(-4-(-2))^(2)+(-4-1)^(2)  } =√(29)` units.

And the length of FG is
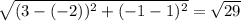`\sqrt{(3-(-2))^(2)+(-1-1)^(2)  } =√(29)` units.

Hence, GO = OL = LF = FG =
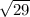`√(29)` units

Now, the slope of line GO is given by
`(-1-(-6))/(3-1) =(5)/(2)`.

Again the slope of OL is given by
`(-6-(-4))/(1-(-4)) =-(2)/(5)`

So, the product of the slopes of GO and OL is =
`(5)/(2)*(-(2)/(5) ) =-1`

Hence, GO ⊥ OL and ∠GOL = 90°

Therefore, it is proved that GOLF is a square. (Answer)