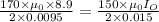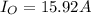Question

Two circular coils are concentric and lie in the same plane. The inner coil contains 170 turns of wire, has a radius of 0.0095 m, and carries a current of 8.9 A. The outer coil contains 150 turns and has a radius of 0.015 m. What must be the magnitude of the current in the outer coil, such that the net magnetic field at the common center of the two coils is zero?

Answer 1

Current in outer circle will be 15.826 A

Step-by-step explanation:

We have given number of turns in inner coil
`N_I=170`

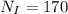
Radius of inner circle
`r_i=0.0095m`

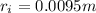
Current in the inner circle
`I_i=8.9A`

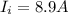
Number of turns in outer circle
`N_o=150`

Radius of outer circle
`r_o=0.015m`

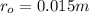
We have to find the current in outer circle so that net magnetic field will zero

For net magnetic field current must be in opposite direction as in inner circle

We know that magnetic field is given due to circular coil is given by

`B=(N\mu _0I)/(2r)`

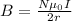
For net magnetic field zero

`(N_I\mu _0I_I)/(2r_I)=(N_O\mu _0I_0)/(2r_O)`

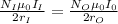
So
`(170* \mu _0* 8.9)/(2* 0.0095)=(150* \mu _0I_O)/(2* 0.015)`

`I_O=15.92A`