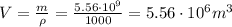Question

In 2006, the United States produced kilowatt-hours (kWh) of electrical energy from 4138 hydroelectric plants (1.00 kWh = J). On average, each plant is 90% efficient at converting mechanical energy to electrical energy, and the average dam height is 50.0 m. As water flows through the hydroelectric plant apparatus, it maintains constant speed all the way to the bottom. a) What was the average power output per hydroelectric plant, for the year of 2006? b) What was the volume of water that flowed over each dam during 2006? (The density of water is 1000 .)

Answer 1

Missing data in the problem:

"..the United States produced
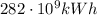`282\cdot 10^9 kWh` of electrical energy.."

a) 77.8 kW

Here we are given the total energy produced by the 4138 power plants. In fact, the total energy produced is

`E=2.82\cdot 10^9 kWh`

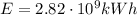
And converting into Joules:

`E=(2.82\cdot 10^9)(3.60\cdot 10^6)=1.02\cdot 10^(16) J`

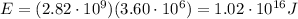
We know that this energy has been produced by

n = 4138

power plants, so the average energy produced by each power plant in 1 year was

`E_1 = (E)/(n)=(1.02\cdot 10^(16)J)/(4138)=2.45\cdot 10^(12) J`

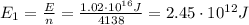
The time in 1 year is:

`t=1 \cdot 365 \cdot 24 \cdot 60 \cdot 60 =3.15\cdot 10^7 s`

So, the average power output of each power plant was

`P=(E_1)/(t)=(2.45\cdot 10^(12))/(3.15\cdot 10^7)=7.78\cdot 10^4 W = 77.8 kW`

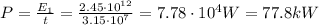
b)
`5.56\cdot 10^6 m^3`

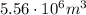
We said that the energy output of each power plant in 1 year is

`E_1=2.45\cdot 10^(12) J`

But we also know that each plant is 90% efficient, so the actual initial mechanical energy due to the volume of water in the dam is

`E=(E_1)/(0.90)=2.72\cdot 10^(12) J`

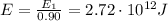
This is the amount of energy stored in the water in each dam. As the water falls down, the initial gravitational potential enegy is converted into electrical energy. The initial gravitational potential energy of hte water is

`E=mgh`

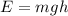
where

m is the mass of the water

`g=9.8 m/s^2` is the acceleration of gravity

h = 50.0 m is the height of the water

Solving for m,

`m=(E)/(gh)=(2.72\cdot 10^(12))/((9.8)(50.0))=5.56\cdot 10^9 kg`

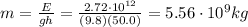
And since the density of water is

`\rho = 1000 kg/m^3`

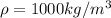
The total volume of water in each dam was

`V=(m)/(\rho)=(5.56\cdot 10^9)/(1000)=5.56\cdot 10^6 m^3`